answers – Reverberations in Mathematics

As an introductory remark for this being my first set of problems from the Munkres text, I have a few things to note.

The numbering system corresponds as follows: “<chapter>.<section>.<problem number>”.
Please feel free to correct any mistakes that I make in the comments and I will update them, as I am doing this for my benefit and the readers benefit as well.
The schedule for these posts will solidify for every Monday at $3$ AM PST.
You can find Munkres’s Topology in the References section on my blog if you need a quick link to the text at your convenience.

For this problem set, I am sorry it has only two problems. I will try to post a few more following up in the middle of the week so that can everyone see more. If not, we will start fresh next week.

2.13.1

Problem: Let $X$ be a topological space; let $A$ be a subset of $X$ . Suppose that for each $x\in A$ there is an open set $U$ containing $x$ such that $U\subset A$ . Show that $A$ is open in $X$ .

Answer: Let $U_x$ denote the open set where $x\in U_x\subset A$ . For each $x\in A$ , there will be an open set $U_x$ associated with it. Therefore $\bigcup_{x\in A}U_x=A$ . By the definition of an open set, $A$ is an open set by the fact that the union of opens sets forms an open set. $\blacksquare$

2.13.3

Problem: Show that the collection $\mathcal{T}_C$ given in Example $4$ of Section $12$ is a topology on set $X$ . Is the collection

$\mathcal{T}_\infty=\{U|X-U$ is infinite or empty or all of $X\}$

a topology on $X$ ?

Answer: By the definition of a topology,

$X-X=\emptyset$ and $X-\emptyset=X$ ; therefore $X$ and $\emptyset$ are in $\mathcal{T}_C$ .
Let $\{U_\alpha\}_{\alpha\in J}$ be an indexed family on nonempty elements of $\mathcal{T}_C$ . Then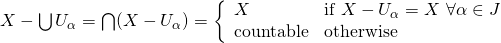Therefore this shows that $\bigcup U_\alpha\in\mathcal{T}_C$ for all $\alpha\in J$ .
And 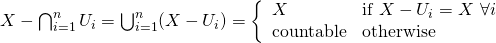Therefore this shows that $\bigcap_{i=1}^n U_i\in\mathcal{T}_C$ for some $i$ .